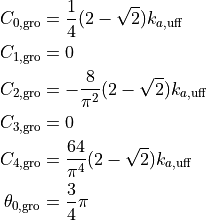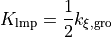11.3. Force Field

11.3.1. Universal Force Field

The Universal Force Field (UFF) available in Winmostar’s molecular dynamics calculations (Gromacs, LAMMPS) is implemented as follows.

First, use OpenBabel’s UFF parameter assignment function to assign parameters to the molecule of interest. Then, for atoms that do not correspond to the atom type described in the original UFF paper [Rappe1992], the Coordination is automatically changed and a closer atom type is assigned. See the OpenBabel source code for more information.

The functional form of UFF cannot be completely reproduced by the functions available in Gromacs and LAMMPS, so the coefficients are converted for the functions available in Gromacs and LAMMPS using the method of OBGMX [Garberoglio2012]. For the Improper torsion, the same harmonic function (improper_style harmonic) is used instead of the LAMMPS improper_style fourier. Improper torsion is calculated using the same harmonic function (improper_style harmonic) as in Gromacs, instead of using the improper_style fourier in LAMMPS.

In addition, fourth-order function is used in Winmostar because the Angle potential in the square planar and octahedral structures does not give a proper stable structure due to the fact that there is only one minuscule point int OBGMX method. The coefficients of the quadratic function were determined by the following policy.

Reproducing the position (angle, energy) of two potential minimum points

Reproducing the energy of a maximum point between two potential minima

In the case of LAMMPS, however, the coefficient of zero order cannot be set, so only the energy is shifted by a constant amount (the force, which is a derivative of the energy, is the same for Gromacs and LAMMPS, so there is no practical effect).

Because of the above policy, the resulting equilibrium structure and distribution is expected to remain largely unchanged from the case using the UFF original potential. Note that the widely used OpenBabel also adds its own penalty function to the Angle potential, which strictly deviates from the UFF original potential.

In Winmostar, the coefficients of Angle for square planer and octahedral are as follows. $C_{i, \mathrm{gro}}$ is the coefficient of Gromacs’ fourth-order function, $k_{a, \mathrm{uff}}$ is the coefficient of UFF; in LAMMPS, only $C_{2, \mathrm{gro}}$ and $C_{4, \mathrm{gro}}$ are used.

$C_{\mathrm{0,gro}} &= \frac{1}{4}(2-\sqrt{2})k_{a,\mathrm{uff}} \\ C_{\mathrm{1,gro}} &= 0\\ C_{\mathrm{2,gro}} &= - \frac{8 }{\pi^2} (2-\sqrt{2})k_{a,\mathrm{uff}}\\ C_{\mathrm{3,gro}} &= 0\\ C_{\mathrm{4,gro}} &= \frac{64 }{\pi^4}(2-\sqrt{2})k_{a,\mathrm{uff}} \\ \theta_{0,\mathrm{gro}} &= \frac{3}{4}\pi\\$

Also, the calculation of Improper torsion angle in Gromacs depends on the order of particle indices (jkl) (LAMMPS does not). Therefore, Winmostar automatically adjusts the index order so that the results in Gromacs and LAMMPS are consistent. (For details, see Gromacs to LAMMPS force field file conversion)

[Rappe1992]
A.K. Rappe, C.J. Casewit, K.S. Colwell, W.A. Goddard III and W.M. Skiff, J. Am. Chem. Soc., 114 (1992), 10024–10035.

[Garberoglio2012]

Garberoglio, J. Comp. Chem., 33 (2012), 2204-8.

11.3.2. Dreiding

Dreiding, which is available in Winmostar’s molecular dynamics calculations (Gromacs, LAMMPS), is implemented as follows.

As for Improper torsion, Gromacs does not implement the function for dreiding, so I use harmonic (funct=2) in Gromacs and improper_style umbrella in LAMMPS to calculate it.

In Winmostar, the coefficients are converted as follows. $k_{\xi, \mathrm{gro}}$ are the coefficients of Gromacs and $K_{\mathrm{lmp}}$ are the coefficients of LAMMPS. We adopt the form of the Taylor expansion at the potential minima, ignoring after the fourth-order terms.

$K_{\mathrm{lmp}} &= \frac{1}{2} k_{\xi,\mathrm{gro}} \\$