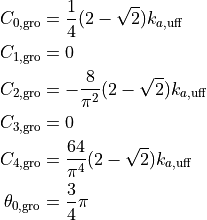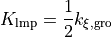11.3. 力場に関して

11.3.1. Universal Force Field

Winmostarの分子動力学計算（Gromacs, LAMMPS）で利用できるUniversal Force Field（以下、UFF）は次のように実装されています。

まず、OpenBabelのUFFパラメータアサイン機能を利用して、対象となる分子にパラメータをアサインします。その際に、UFFの原著論文 [Rappe1992] に書かれたatom typeに相当しない原子については、Coordinationを自動で変更して近いatom typeがアサインされます。詳細は、OpenBabelのソースコードを参照してください。

UFFの関数形はGromacs、LAMMPSで使用可能な関数で完全に再現することができません。そのため、OBGMX [Garberoglio2012] の方法でGromacsおよびLAMMPSで使用可能な関数向けに係数を変換しています。Improper torsionについては、LAMMPSのimproper_style fourierを使わず、Gromacsと同じharmonic関数（improper_style harmonic）で計算しています。

また、OBGMXの方法では、square planar、octahedral構造におけるAngleポテンシャルで、極小点が1か所しかないために適切な安定構造を与えないため、Winmostarでは4次関数を使用しています。4次関数の係数は、以下の方針で決定しました。

2か所のポテンシャル極小点の位置（角度、エネルギー）を再現する

2か所のポテンシャル極小点の間にある極大点のエネルギーを再現する

ただし、LAMMPSの場合は0次の係数を設定できないため、エネルギーのみ定数分シフトする（エネルギーの微分である力はGromacsとLAMMPSで一致するので、実用上の影響はないと思われる）

上記の方針のため、得られる平衡構造と分布はUFF原著のポテンシャルを使った場合から大きく変化しないと期待されます。なお、広く使われているOpenBabelにおいても、Angleポテンシャルに独自のペナルティ関数を追加しており、厳密にはUFF原著のポテンシャルからずれがあります。

Winmostarではsquare planer, octahedralのAngleの係数を以下のようにしました。 $C_{i, \mathrm{gro}}$ はGromacsの4次関数の係数、 $k_{a,\mathrm{uff}}$ はUFFの係数です。LAMMPSの場合は $C_{2, \mathrm{gro}}$ と $C_{4, \mathrm{gro}}$ だけが使われます。

$C_{\mathrm{0,gro}} &= \frac{1}{4}(2-\sqrt{2})k_{a,\mathrm{uff}} \\ C_{\mathrm{1,gro}} &= 0\\ C_{\mathrm{2,gro}} &= - \frac{8 }{\pi^2} (2-\sqrt{2})k_{a,\mathrm{uff}}\\ C_{\mathrm{3,gro}} &= 0\\ C_{\mathrm{4,gro}} &= \frac{64 }{\pi^4}(2-\sqrt{2})k_{a,\mathrm{uff}} \\ \theta_{0,\mathrm{gro}} &= \frac{3}{4}\pi\\$

また、GromacsにおけるImproper torsion angleの計算は粒子のインデックスの順番（jkl）に依存します（LAMMPSは依存しない）。そのため、Winmostarはインデックスの順番を自動調整し、GromacsとLAMMPSでの計算結果が一致するようにしています。（詳細は Gromacs→LAMMPSの力場ファイル変換）

[Rappe1992]
A.K. Rappe, C.J. Casewit, K.S. Colwell, W.A. Goddard III and W.M. Skiff, J. Am. Chem. Soc., 114 (1992), 10024–10035.

[Garberoglio2012]

Garberoglio, J. Comp. Chem., 33 (2012), 2204-8.

11.3.2. Dreiding

Winmostarの分子動力学計算（Gromacs, LAMMPS）で利用できるDreidingは次のように実装されています。

Improper torsionについては、GromacsでDreidingの関数が実装されておらず、Gromacsではharmonic (funct=2)、LAMMPSではimproper_style umbrellaで計算するようにしています。

Winmostarでは以下のように係数を変換しています。 $k_{\xi, \mathrm{gro}}$ はGromacsの係数、 $K_{\mathrm{lmp}}$ はLAMMPSの係数です。ポテンシャル極小点におけるテーラー展開の4次項以降を無視した形式を採用しています。

$K_{\mathrm{lmp}} &= \frac{1}{2} k_{\xi,\mathrm{gro}} \\$